مقاله حاضر نسخه اصلاح شدهای از حریم خصوصی تفاضلی اولیه بر مبنای Rényi divergence ارائه کرده است. تا پیش از این نسخههای سهلگیرانهتری برای حریم خصوصی تفاضلی نظیر ε,δ)-Differential Privacy) نیز معرفی شده است. در این مقاله نشان داده شده که تمام ویژگیهای حریم خصوصی تفاضلی اولیه برای این تعریف نیز قابل اثبات است. همچنین این تعریف اجازه طراحی فرآیندهای حریم خصوصی با عملکرد بهتری در شرایط ترکیب را نسبت به نسخههای پیشین ارائه میدهد.
Divergance در آمار و نظریه اطلاعات، نمایش دهنده نوعی فاصله میان توزیعهای احتمالی میباشد. در این مقاله سعی شده است با ارائه مفهوم Rényi divergence میان دو توزیع احتمالی، از آن برای نمایش حریم خصوص تفاضلی استفاده کند. از این رو برای دو توزیع احتمال P و Q که رو دامنه R تعریف شدهاند، Rényi divergence با درجه α>1 به صورت زیر تعریف میشود:
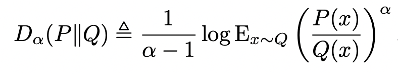
زمانی که α به سمت بینهایت میل کند، این تعریف همان تعریف حریم خصوصی تفاضلی عمومی خواهد بود. براساس این مفهوم، Rényi Differential Privacy با نماد α,ε)-RDP)، به صورت زیر تعریف میشود:
یک فرآیند تصادفی f:D –> R حریم خصوصی تفاضلی Rényi را با مرتبه α در صورتی رعایت میکند که نامساوی زیر برقرار باشد:
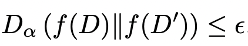
در این مقاله ثابت شده که تمام ویژگیهای حریم خصوصی تفاضلی عمومی در این تعریف نیز برقرار است. جدول زیر مقایسهای میان این ویژگیها برای دو تعریف حریم خصوصی تفاضلی اولیه و Rényi را نشان میدهد.

همانگونه که در جدول فوق نمایش داده شده ، به میزان توان اضافه شده در تعریف، قابلیت تحمل خطا در حریم خصوصی تفاضلی Rényi افزایش یافته است.
نتایج به دست آمده در این مقاله نشان میدهد که این تعریف میتواند حد بالای بسیار محدودتری در زمینه نسبت احتمالی میان دو مجموعه داده همسایه به ازای احتمال اولیه مختلف در فرآیندهای ترکیبی نسبت به روشهای پیشین حفظ حریم خصوصی تفاضلی ارائه دهد.
در این مقاله از مفاهیم مختلف نظریه اطلاعات از قبیل نامساویهای ینسن،نظریه مارکف و نیز فاصله divergence استفاده شده که قابل توجه است.
I. Mironov, “Rényi Differential Privacy,” 2017 IEEE 30th Computer Security Foundations Symposium (CSF), 2017, pp. 263-275, doi: 10.1109/CSF.2017.11.