سازوکارهای حریم خصوصی تفاضلی

در تعریف حریم خصوصی تفاضلی سراسری و حریم خصوصی تفاضلی محلی از سازوکارها استفاده شده است. سازوکارهای متفاوتی برای استفاده در حریم خصوصی تفاضلی ارائه شده‌اند که هرکدام ویژگی‌های خاص و منحصر بفرد دارند. قبل از اینکه به معرفی سازوکارها بپردازیم، ابتدا با مفهوم حساسیت سراسری آشنا خواهیم شد.

حساسیت سراسری

حساسیت (Sensitivity) [1] یک مقدار است که تعیین می‌کند برای یک پرس‌وجوی خاص در یک سازوکار چه میزان آشفتگی (Perturbation) نیاز است. حساسیت به صورت زیر تعریف می‌شود.

برای تابع \(f: D \rightarrow R\)، و مجموعه‌داده‌های همسایه D و ’D، حساسیت f به صورت زیر تعریف می‌شود:

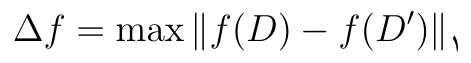
مقدار حساسیت برابر با حداکثر اختلاف بین پاسخ پرس‌وجوها در دو مجموعه‌داده همسایه می‌باشد که بیان می‌کند با حضور یا عدم حضور یک عضو از داده، در خروجی پرس‌وجو چه میزان تغییرات خواهیم داشت. به عنوان مثال، حساسیت تابع شمارش سطر همیشه برابر با یک می‌باشد. تلاش بر این است که این مقدار کمینه شود.

سازوکارها

همانطور که اشاره شد، برای حریم خصوصی تفاضلی سازوکارهای متفاوتی ارائه شده است. این سازوکارها قابلیت ترکیب شدن و شخصی‌سازی را نیز دارند. در این بخش به معرفی چند سازوکار خواهیم پرداخت.

سازوکار لاپلاس

سازوکار لاپلاس (Laplace) [1] به پاسخ خام دریافت شده از سرپرست داده، مقداری نوفه مستقل از اندازه مجموعه‌داده اضافه می‌کند. \(Lap(\frac{\Delta f}{\epsilon})\) برای نمایش نوفه نمونه برداری شده از توزیع لاپلاس استفاده می‌شود. این سازوکار قادر به ارائه پاسخ برای پرس‌وجوهای غیر عددی نیست و برای پرس‌وجوهای دارای حساسیت کم عملکرد خوبی دارد. همچنین مقدار 𝛿 همیشه برابر با صفر است.

برای تابع \(f: D \rightarrow R\) بر روی مجموعه داده D، سازوکار M که به صورت زیر تعریف می‌شود، حافظ حریم ‌خصوصی ‌تفاضلی با عامل ε است.

\(M(D) = f(D) + Lap(\frac{\Delta f}{\epsilon})\)

این تعریف بیان می‌کند که هر چقدر مقدار ε کمتر باشد، مقدار نوفه اضافه شده به پاسخ درست بیشتر خواهد بود و در نتیجه بودجه و سطح حریم خصوصی تفاضلی بیشتر خواهد شد. همچنین وجود حساسیت تابع f در صورت کسر بیان کننده این است که هر چه حساسیت تابع کمتر باشد، نوفه کمتری نیز برای حفاظت از حریم خصوصی داده‌ها مورد نیاز است.

سازوکار نمایی

سازوکار نمایی (Exponential) [2] معمولا برای هر دو نوع داده عددی و غیرعددی استفاده می‌شود. از این سازکار زمانی استفاده می‌شود که نیاز است به پرسشگر، پاسخ بدون نوفه داده شود. به عبارت دیگر پاسخ پرس‌وجو عضو مجموعه R می‌باشد و نوفه حریم خصوصی تفاضلی، در انتخاب آن اثر دارد و به صورت مستقیم به پاسخ اضافه نمی‌شود. به عنوان مثال افزودن نوفه به پاسخ سوال «کدام دانشگاه تعداد دانشجویان ورودی کارشناسی ارشد آن بیشتر است؟» بی‌معنا است.

فرض کنید \(q(D, \phi)\) تابع سود مجموعه‌داده D باشد که کیفیت خروجی \(\phi\) را اندازه‌گیری می‌کند و \(\Delta q\) حساسیت را نمایش می‌دهد. سازوکار نمایی M حافظ حریم ‌خصوصی ‌تفاضلی با عامل ε است اگر:

\(M(D) = return \phi \propto exp(\frac{\epsilon q(D, \phi)}{2 \Delta q})\)

هزینه حریم خصوصی این سازوکار مستقل از اندازه مجموعه R است. از آن می‌توان برای مجموعه‌های متناهی و نامتناهی استفاده نمود. البته در مرحله پیاده‌سازی چالش‌هایی برای مجموعه‌های نامتناهی وجود دارد. معمولا می‌توان با تعریف یک تابع سود مناسب، بقیه سازوکارها را بر اساس سازوکار نمایی تعریف نمود.

سازوکار پاسخ تصادفی

سازوکار پاسخ تصادفی (Randomized response) [3] از مفهوم انکارپذیری استفاده می‌کند. فرض کنید قصد دارید پاسخ سوال «آیا شما در ترم گذشته مشروط شده‌اید؟» را بدهید. ابتدا یک سکه را پرتاب می‌کنید، اگر روی سکه آمد جواب شما «بله» و اگر پشت سکه آمد جواب شما حقیقت است. با استفاده از این فرآیند به انکارپذیری قوی برای پاسخ «بله» دست می‌یابیم، به صورتی که پاسخ‌دهنده می‌تواند ادعا کند پاسخ «بله» حاصل از روی سکه آمدن است، نه بیان حقیقت. این سازوکار را می‌توان با پرتاب یک سکه دیگر توسعه داد تا انکارپذیری برای پاسخ «خیر» نیز ایجاد شود. سازوکار پاسخ تصادفی با ایجاد انکارپذیری با استفاده از پرتاب دو سکه، نشان می‌دهد که حدود ۷۵ درصد پاسخ‌ها «بله» هستند. بنابراین حافظ حریم‌ خصوصی ‌تفاضلی با عامل ε و با مقدار ε = ln(3) می‌باشد. [4]

سازوکار گاوسی

سازوکار گاوسی (Gaussian) [5] شبیه سازوکار لاپلاس است که بجای افزودن نوفه توزیع لاپلاس، نوفه توزیع گاوسی را به داده‌ها اضافه می‌کند. بنابراین می‌توان از آن‌ها در روش‌های یکسانی استفاده و برای εهای مختلف عملکرد و خروجی آن‌ها را مقایسه نمود.

برای تابع \(f: D \rightarrow R\) بر روی مجموعه داده D، سازوکار M که به صورت زیر تعریف می‌شود، حافظ حریم ‌خصوصی ‌تفاضلی با عامل (ε, 𝛿) است.

\(M(D) = f(D) + N(\frac{2 \Delta f^2 log(1.25 / \delta)}{\epsilon^2})\)

در تعریف بالا از تابع N برای نمایش نوفه نمونه برداری شده از توزیع گاوسی استفاده شده است. در تعریف بالا مشاهده می‌شود که از 𝛿 در مخرج کسر استفاده شده است، بنابراین مقدار 𝛿 نمی‌تواند صفر باشد و در نتیجه سازوکار گاوسی از حریم‌ خصوصی تفاضلی محض پشتیبانی نمی‌کند.

[1] Dwork, Cynthia. “A firm foundation for private data analysis.” Communications of the ACM 54.1 (2011): 86-95.

[2] McSherry, Frank, and Kunal Talwar. “Mechanism design via differential privacy.” 48th Annual IEEE Symposium on Foundations of Computer Science (FOCS’07). IEEE, 2007.

[3] Warner, Stanley L. “Randomized response: A survey technique for eliminating evasive answer bias.” Journal of the American Statistical Association 60.309 (1965): 63-69.

[4] Erlingsson, Úlfar, Vasyl Pihur, and Aleksandra Korolova. “Rappor: Randomized aggregatable privacy-preserving ordinal response.” Proceedings of the 2014 ACM SIGSAC conference on computer and communications security. 2014.

[5] Dwork, Cynthia, et al. “Calibrating noise to sensitivity in private data analysis.” Theory of cryptography conference. Springer, Berlin, Heidelberg, 2006.